こんにちは。
ついに化学基礎で学ぶ、基本法則が終了します。このアボガドロの分子説は、これまで矛盾していた「原子説」と「気体反応の法則」の両方を説明できる画期的な仮説でした。

そして、現代を生きる僕たちはこのアボガドロの分子説の結末をよく知っています。現代化学で分子は完全に受け入れられています。かなり精度の高い仮説だったことがわかりますよね。
てな訳で、今回はアボガドロの分子せつをバッチリ紹介します。このアボガドロの分子説はドルトンの「原子説」からゲーリュサックの「気体反応の法則」までの歴史を知っている方がわかりやすいです。
全く、原子説や気体反応の法則のことを知らない人は、まずはこちらを読んでおくことをオススメします。
目次
アボガドロの分子説とは?
1811年アボガドロによって発見された。
①それぞれの気体は、何個かの原子が結合した分子という粒子からできている。
②全ての気体は、同温・同圧のとき、同体積中には同数の分子を含む。
ちなみに、入試に年代までは出ませんが、原子説と気体反応の法則の後に発表されたことがわかっていたらいいでしょう。
分子説までは、水素、酸素、窒素、塩素のような元素がそのまま単体として存在する気体は、単原子で気体だと思われていました。HClのような陽性のHと陰性のClが結合するのはわかるが、陽性同士、陰性同士が結合するわけがないと思われていたからです。
ゲーリュサックが「同温同圧下では、同体積の気体は同数の原子または複合原子を含む」と仮定しました。(後にアボガドロが法則化してアボガドロの法則と呼ばれる)
そして、同じくゲーリュサックは、気体反応の法則で「同温、同圧下で起こる気体反応は、体積比は整数比になる」となります。これが、原子説と矛盾するのです。
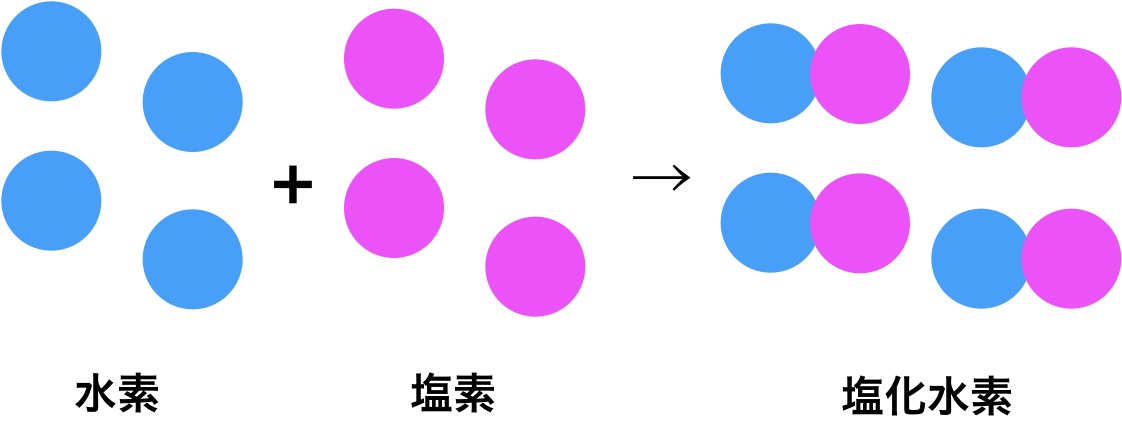
これが、原子説から考えられる水素と塩素の反応です。気体反応の法則で考えると、これの体積比は4:4:4=1:1:1になるはずでした。
しかし、現実は違いました。水素、塩素、塩化水素の体積比は4:4:8=1:1:2になったのです。

このような点で原子説と気体反応の法則は矛盾し合っていました。これを解決したのが分子説です。
この水素と塩素のつぶつぶが、実は2原子からできる分子なんじゃないか? と主張したんです。

このように、水素と塩素の正体が分子だとすると、気体反応の法則と原子説の矛盾はなくなります。
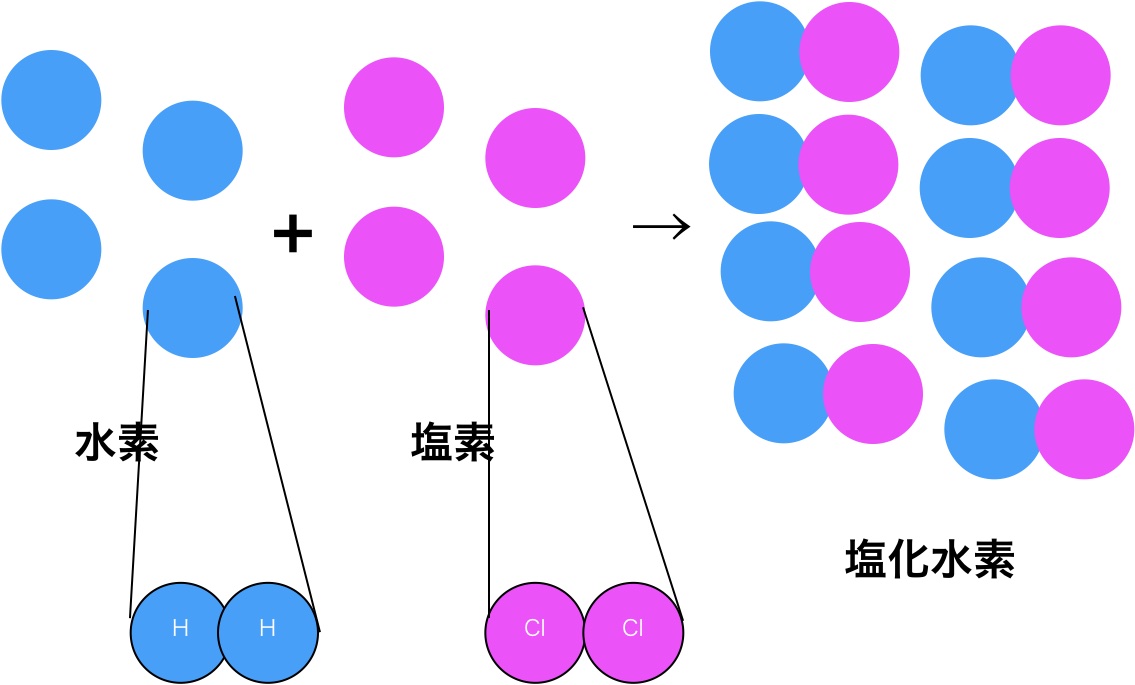
このように、粒子が2粒の原子からできていると唱えたんです。すると、塩化水素の個数も8粒子となり、4:4:8の気体の体積比が成り立ちます。
これで原子説と気体反応の法則が無事に満たされました。またこのおかげで正しい原子量などの測定も進むはずでした。
当時はアボガドロの分子説は実験結果を絡めたものではありませんでした。さらに同温同圧で同体積には同じ個数の気体粒子が存在するという仮定も認められていませんでした。
さらにH-HやCl-Clのように、陽性同士の原子同士が結合するなんてありえないと思われていたので、分子説はアボガドロが生きている間に認められることはありませんでした。
アボガドロの法則の現在
アボガドロの分子説の②の内容は、今では「アボガドロの法則」と言われています。これって混合気体の分野で死ぬほどよく使います。混合気体の分野では、分圧、分体積を使いますよね。(まだ習っていない人はわからなくてOK)
これを、状態方程式で表すと、PV=nRTで、同温同圧だとすると、P,T一定なのでV=knです。これが表すのは、分体積はモルに比例するという内容です。

ってことです。これがアボガドロ定数を現代風に表したものです。
最後に
化学の基本法則はこれで全て扱い終えました。この分子説って実は現代化学においても正しいものが多いので、案外分子説についてとやかく聞かれることは少ないです。
重要なのは、アボガドロの法則をきっちり気体計算で使えることです。
基本法則は、「アボガドロ 分子説」と唱えるように覚えても全く面白くないし、全く頭に入らないでしょう。
よって、きっちり歴史の流れを学んでみてください。歴史だけをおった記事をまとめてみましたので、こちらをご覧ください。
いかがでしたか? 化学基礎で習う化学の基本法則の内容ですが、それぞれきっちり区別できるようにしてくださいね。当然理論化学や有機化学の問題の方が重要ですが、こういうところで無駄な失点をしないように気をつけてください。