面心立方格子と六方最密構造は、1つの単位格子では配位数がわかりません。なのである特殊な方法を使わないと配位数を求められません。
今日は、その面心立方格子と六方最密構造の配位数を求める考え方をご紹介します。ちなみに、結論から言うと「単位格子を並べる」ことです。
2つの単位格子を並べることで、配位数を求めることができます。
※今回の記事は、超ピンポイントな説明なので文量がそれほどありません。1分ほどで読み終わることができるでしょう。最後まで読んで、時間がありましたら面心立方格子、六方最密構造についての別記事も学んでおいてください。
目次
【結論】面心立方格子と六方最密構造の配位数を求める考え方

面心立方格子も六方最密構造も配位数を求めたければ、単位格子を重ねろ!
これです。上の画像のように面心立方格子は左右に2つ単位格子を重ねます。六方最密構造は上下に2つの単位格子を重ねます。すると、同じ距離の原子がわかります。
面心立方格子の配位数の求め方

面心立方格子を横に2つ並べる
面心立方格子は、赤色の周りに12個の青色の原子があります。このような赤色原子と青色原子を取り出してみます。↓

このように、正方形で見るとわかりやすいです。
六方最密構造の配位数の求め方
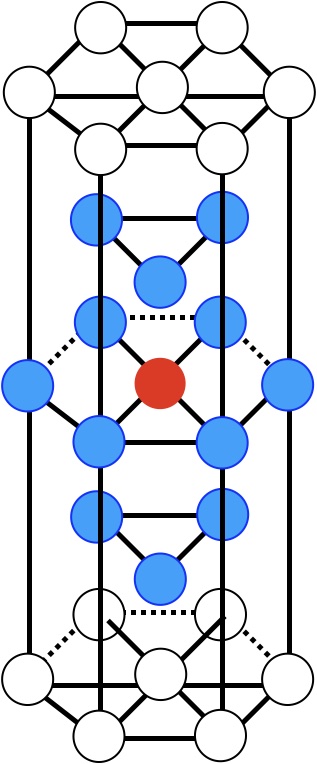
六方最密構造を縦に2つ並べる
このように六方最密構造は上下に2つ並べると、赤色の原子の周りに何個同じ距離で接しているかがわかります。

この周りの6個と、この上のスキマに置かれる上下3個ずつ

これで12配位となります。
面心立方格子と六方最密構造の配位数は最終的には覚えましょう

面心立方格子は立方最密構造と言う別名もあります。面心立方格子と六方最密構造は両方とも最密構造なのです。そしてそれが12配位なんですよ。
12配位が最密構造であると言うことと、六方最密構造と面心立方格子は両方とも最密構造であり、12配位であることは化学を勉強する人間として常識です。なので、これは覚えてしまっていいでしょう。
まとめ
- 面心立方格子と六方最密構造の配位数は、単位格子を2つ並べて求める。
- 2つとも最密構造で12配位であることは覚える
実際、一度どのようになっているのかを理解した上で最終的に覚えてしまいましょう。一度理解することで、勉強したことが頭に入りやすくなりますから。
このような単位格子は、問われることが決まっているので、問われる内容は全て瞬時に導き出せるようにしておくべきです。配位数もそのうちの1つです。
結晶系は問われることがたった5つなので、ぜひみてみてください。














