こんにちは。
結晶の問題の中で最も出題されるのが、面心立方格子です。とはいえ、別に難しくありません。今回の記事を読めば、面心立方格子の問題で入試で問われるのがたった5つだけだと言うことがわかるでしょう。
そのほか、
- 面心立方格子の求め方
- 面心立方格子の配位数の考え方
- 金属結晶以外でも面心立方格子はあるのか?
※演習問題を除けば2分ほどで読み終われます。もし時間があれば演習問題も最後取り組んでみてください。
目次
面心立方格子とは?

これが面心立方格子です。

このように、面の中心に原子があります。面の中心に原子がある立方格子だから面心立方格子です。
面心立法格子で出題されるのはたった5つ
- 単位格子内の原子数
- 配位数
- 原子半径と単位格子の1辺の長さの関係
- 密度
- 充填率
この5つです。また、順番も重要なんですよ。1を求められないと4が求められないし、2が求められないと5も求められないのです。
この5つを難なく求められるようになったら、結晶は余裕になってきます。はっきり言って難しいことは一つもやっていないので、全部マスターしちゃってください。
単位格子内の原子の数
単位格子の頂点にある1/8原子と面の中心にある1/2原子を数えろ!
まず、面心立方格子の単位格子内の原子は、頂点に8個ありますね。

このように1/8個が8箇所にあるので、合計1個です。さらに、面の中心に1/2原子が6箇所にあります。

よって、頂点の1個と面の3個を合わせて面心立方格子に含まれる原子の数は4個です。
配位数

面心立方格子の配位数を調べる時は、単位格子を2つ並べて考える
このように、面心立方格子は1つの単位格子だけだと配位数を数えることができませんので、2つの単位格子を繋げます。すると、画像のように、赤色の原子の周りに青色の原子が同じ距離で12個あります。
なので、面心立方格子は、12配位です。この考え方めちゃくちゃ重要なので、バッチリ覚えておいてくださいね。;
密度
密度は機械的に求めろ! 密度の単位を確認して分子と分母を別々作り出すだけで求められる!
密度は、あまり難しいことを考えずに単位を見て機械的に求めてしまえばいいです。まず密度の単位を考えます。

これが密度の単位ですよね。これを分子と分母で別々に求めていきます。
まずは、分子の質量を求めます。単位格子の質量は含まれている原子の質量ですので、
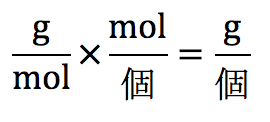
このように、質量を求めます。分子量、アボガドロ定数を使うのですが、難しいことを考えずにgが欲しいから分母のmolを消し、gが欲しいから分母の個を消すだけです。

はっきり言うと単位をいじくっているだけですが、これがもっとも間違えにくい方法です。では、方針ができたのでこれに代入をして行きます。分子量をM、アボガドロ定数をNA、個数は面心立方格子に含まれるのは4個ですよね。代入して

このようになります。これが分子の質量です。分母のcm3(全体)は、単位格子の一片の長さをaとすると、a3で求められます。あとは代入するだけです。よって

このようにして面心立方格子の密度を求めていきます。
単位格子の一辺の長さと原子半径の関係

面心立方格子の、単位格子の1辺の長さと原子半径の関係を考えるときは、面心立方格子の1つの面の対角線で関係を作れ!
上の画像の面心立方格子の1つの面だけを取り出します。

このように面心立法格子の面心の原子を真っ二つに割る、部分で対角線をrとaで表します。この対角線は、rで表すと4rだし、aで表すと三平方の定理より√2aになります。
よって、面心立方格子のaとrの関係は
4r=√2a
になります。
充填率
充填率は単位を覚えて、その単位を分子分母別々に作ろうと考えれば良い

充填率って言うのは、単位格子の体積あたりの原子の体積の割合のことです。なので充填率は単位が

です。この単位の分子と分母を別々に求めていきます。

このrに先ほどの原子半径と単位格子の一辺の長さの関係を用いて、代入します。

このように求めます。途中で、a3は分母分子で打ち消しあって、最終的に数字だけの定数になるんですよ。てことは、これで何が言えるかわかりますか?
面心立方格子の充填率は、なんと原子半径や単位格子の長さに関わらず一定であると言うことです。
こうすると、a3が消えます。よって、充填率は、原子半径や単位格子の一辺の長さも関係ない事がわかります!
面心立方格子をとるのは金属だけではない!

よく、金属結晶のところで、体心立方格子、面心立方格子、六方最密構造を学ぶので、金属しか面心立方格子を取らないのじゃないかと思っている人も多いでしょう。確かに金属でも面心立方格子をとるものは多いです。
最低限これだけは覚えておいてください。
しかし、金属以外でも面心立方格子を取りますよ。分子結晶なんかはよく面心立方格子をとります。
実際に面心立方格子の解法を使ってみよう
銀の結晶は面心立方格子である。以下の問いに答えよ。
(1)単位格子に何個の銀原子が含まれるか。
(2)1個の銀原子に隣接している他の銀原子は何個か。ただし、銀原子は球形で、最も近い原子は互いに接しているものとする。
(3)単位格子の一辺の長さをa[cm],銀の原子半径をr[cm]とするとき、aをrを用いて表す式を書け。
(4)単位格子の一辺の長さをa[cm],銀の原子量をM,アボガドロ定数をNとするとき銀の密度d[g/cm3]を表す式を書け。
(5)原子を球と考えると、球が占めている体積の全体積に対する割合を充填率と言う。最密構造をとる面心立方格子の充填率(%)を有効数字3桁で求めよ。√2=1.41
まとめ
面心立方格子の問題でしたがいかがでしたか? 配位数を求めるときなど若干体心立方格子と違うところもありましたが、基本問われることは同じでたった5つです。
なので、全ての結晶でこれらが求められるようになればもう最強です。













コメントを残す