どうも受験化学コーチなかむらです。
ヘンリーの法則ってなんかとっつきにくくないですか?


おそらくこのような悩みを抱えていることでしょう。それもそのはず! ヘンリーの法則には2つの法則がありますが、それぞれ矛盾している(ように見える)のです。
- 一定温度では気体の溶解度はその気体の分圧に比例する。
- 一定温度では一定体積の溶媒に溶ける気体の体積は圧力によらない。

本記事ではこのような悩みを解決していきます。そしてそれだけではなくヘンリーの法則で入試問題で出てくる計算問題もしっかり溶けるようにしていきます。
はっきり言います。ヘンリーの法則って超簡単です。多くの受験生の悩みの本質は「気体が苦手だと言うこと」です。

目次
ヘンリーの法則自体は超簡単!「押せば溶ける」これだけ
ヘンリーの法則は単純明快です。温度が一定の時に水に溶ける気体の量は気体の圧力(押す力)に比例するというものです。
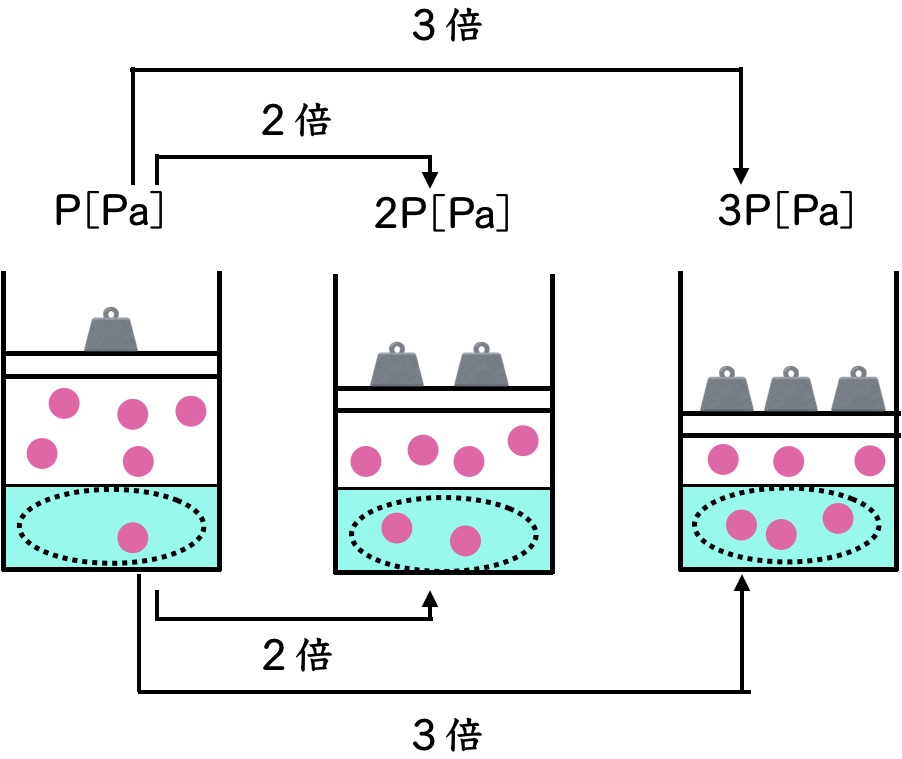
ヘンリーの法則は上のイラストのように2倍押したら2倍溶けますよ〜ってだけの法則なんですよ。これを計算式で表すと、
Aの濃度=kPA
という計算式が成り立ちます。
超重要なことですがヘンリーの法則で論じるのは難容性の気体の溶解度です。アンモニアや塩化水素のような水に溶けやすいものはヘンリーでは論じません。
窒素や酸素のような無極性の気体は水に溶けにくいです。水に溶けにくい気体がいかに水に溶けるかを論じる法則です。

と思った人は鋭いです。このヘンリーの法則でmolが出てこない理由は後ほど解説します。
1.0×105Paが2.0×105Paになったら溶ける量が2倍になるのは当たり前です。倍の力で水の中に気体を押し込んでいるのと同じですからね。
ただし、ここまでで混乱する人はいません。でも、大半の受験生はヘンリーの法則でつまづきます。
その理由が化学の歴史に関係があります。僕らは化学で量を測るとき「mol」を使いますよね。だって、化学反応や化学反応の比はmolで計算しますから。
でも、このヘンリーの法則って実は体積なんですよ。それについて以後解説していきます。
なぜヘンリーの法則が苦手な受験生が多い?
- ヘンリーの法則の2つ目の定義の文章がよくわからん
- ヘンリーの法則と気体の問題の混同
これらの3つの原因でヘンリーの法則を苦手に思う受験生が激増しています。
第1の理由、ヘンリーの法則の2つ目の定義で大混乱
①一定温度では気体の溶解度はその気体の分圧に比例する。
②一定温度では一定体積の溶媒に溶ける気体の体積は圧力によらない。
まず、①は超簡単。先ほど説明した通り、『押せば溶ける』ですね。Aという気体だとすると、
Aの濃度=kPA
これだけなのです!
だから圧力が2倍になれば2倍溶けるのです。これは先ほど説明した通りです。
問題は②です。押せば解けるのに、気体の体積は圧力によらないと言う意味です。

ってブチギレているところでしょう。実はこれには理由があります。
この記述の意味がわからずイメージがつかないのは歴史のせいだと言えます。少し重要な年表をご紹介します。
| 年代 | 出来事 |
| 1803年 | ウィリアム・ヘンリーがヘンリーの法則を発表 |
| 1853年 | オストワルト生まれる |
ここでもう一度ヘンリーの法則の2つ目の定義を確認しますね。
②一定温度では一定体積の溶媒に溶ける気体の体積は圧力によらない。
そう、気体の”体積”で語っているところがややこしくしているポイントです。無意識のうちにあなたはこの体積をまるでmolかのように考えていませんでしたか?

そう、だからヘンリーの法則は、気体の溶解量を気体の体積で表現せざるを得なかった。
なので多くのヘンリーの法則の問題は未だに気体の溶解量を体積で、求めろと言わんばかりの問題ばかりです。
たとえば以下の問題を見てみましょう。
モルが少しもでてこないですよね。
ですが、僕らは普通にmolを知っているし、理論化学の問題を解くための基本は『モルに変換して、モル比で関係式を作ること』でした。(関連記事:理論化学の計算なんて簡単!2つの事を意識するだけで解ける!)
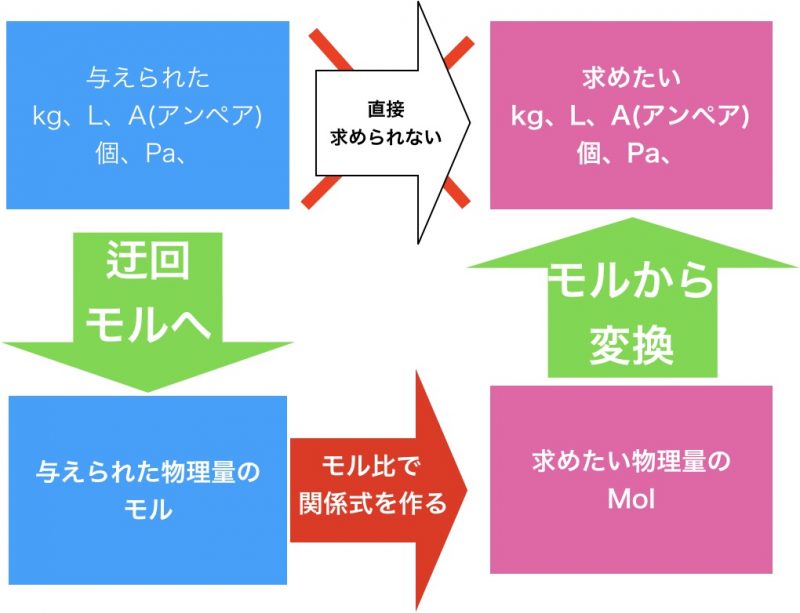
「モル」は体積を聞かれても、質量を聞かれても、すぐに変換できて便利です。そして化学計算の基本は、『モル利用』だということも、様々なところで述べてきました。
この2つ目の定義が意味わからん人が多いです。ですが、普通に考えて大丈夫です
V=nRT/P
V=2nRT/2P=nRT/P
ですよね。てことは、圧力が2倍ならmolは2倍なんです。ですが、体積は同じなんですよ。
なので、本記事ではヘンリーの法則を「mol」で解く教科書にも載っていない最強の解法をあなたにインストールします。
第2の理由:ヘンリーの法則で悩んでいない
先ほどの例題を出しますね。こんな問題がヘンリーの法則では出題されます。こういう問題で圧力が1.0×105Pa

水に溶けてる気体の量を知る以外の役割はありません。
待て待て、それはただの気体の反応だろ?

ここだけ取り出してみてくださいよ。普通に気体の問題じゃないですか。でもヘンリーの法則の問題になると、
これは、ヘンリーの法則が「水に溶けている気体の量を知る以外の役割がない」ということをちゃんと認識していないからです。
ヘンリーの法則は水に溶けている気体の量を知る以外の役割はない。

という質問が死ぬほどきます。これは、完全にヘンリーの法則ではなく気体の問題で間違っています。
ヘンリーの法則は水に溶けている気体を取り出す以上でも以下でもありません!!!!
これめっちゃ重要ですよ!


多くの人は『問題点の分離』ができていないんだよ。みんなが苦手なのはヘンリーの法則ではなく、気体の法則の扱い方だったりしますね。
これを例題を交えて解説していきますね。
「気体の圧力を変えたときの体積の求め方」とか「体積が変化したときの圧力や温度」などの変換が苦手で不安な人は、以下の記事で確認しておいてくださいね!
ヘンリーの法則はモルで計算せよ!ヘンリーの法則最強の攻略法
ヘンリーの法則の文章をそのまま公式にすればいいんですよ!
ヘンリーの法則は押せば溶けるでしたよね!このときの溶ける量を『モル』にしたいわけですよ!
[A]=kPA
Aという気体が溶ける量をnA、Aの分圧をPAとします。
nAはPAに比例しますので、nA=kPA(kはヘンリー定数と言います)と書けます。
また、当然ながら、1Lの水と5Lの水で溶ける気体の量はどうなるかと言うと、5倍になりますよね!これから、水の体積にも比例しますので、水の体積をV水とすると
nA=kPAV水
という式が書けるわけです!
これがヘンリーのモルを求める公式なんです!ここからは全てこの公式に当てはめてまずモルを求めてしまってください!
「これ本当にこの公式で良いの?」って思うかもしれません。
「なかむらの妄想の公式じゃねえの!」っておもって使うのが不安になる人も居るかもしれません。
大丈夫です!これは実在する解法です!
では、この公式を実際に導きだす過程をご覧いただきましょう。証明ではないけど、納得してもらえると思います。
先ほどもありましたが、ヘンリーの法則は昔濃度で表されていましたね。気体Aとおくと、
[A]=kPA
と表せます。[A]はモル濃度のことです。
そして、この[A]ですが、[A]=nA/V(全)です。しかし、このL(全)ですが、V(全)=V(水)+V(溶質)ですよね。
このV(溶質)というのは、よく考えてください。ヘンリーの法則というのは、『あんまり溶けない気体』が水に溶けるときどれくらい溶けるの?っていうのをまとめた法則ですよ!
先ほど、アンモニアや塩化水素が水に溶けるかを表す法則ではなく、窒素や酸素のような気体が水にどれくらい溶けるかを表す法則だと説明しました。
つまり、溶質の体積V(溶質)はゴミレベルです。だって、溶質って雑魚だから
だから、V(全)≒V(水)としていいのです!これを用いて、ヘンリーの法則を表すと下のようになります!

この式に両辺V水を掛けると、、
nA=kPAV水
このように、導けます。では次にこれを具体的にどうやって使うかを解説していきます。
ヘンリーの法則の問題のmolを使った解法を解説
ステップ1:問題文を整理する(表にまとめる)
ステップ2:『ヘンリーモル変換公式』からヘンリー定数を求める
ステップ3:『ヘンリーモル変換公式』からモルを求める。
ステップ4:モルから求める状態量を求めていく!
この流れを踏めばヘンリーの法則の問題を解くことはできます。これをしっかり頭に入れてください。
ここまで聞いただけでは使いこなすことはできないと思うので、具体的に例題で解説していきます。
先ほどの問題です。
『ヘンリーモル変換公式』で問題を解く場合は、
nA=kPAV水
の公式を起点に求めていきます。
nAは条件文の水に溶けている気体の物質量
PAは条件文の気体Aの分圧
V水は溶媒の水の体積
このkがあたえられていることは滅多にありません。なので、このkを求めることをまず考えます。
水温が一定ならヘンリー定数は一定!となります。これを利用して、問題を解いてみましょう。
こちらの動画でご確認ください。
この動画で解説しているようにステップバイステップで解いていきます。l
ステップ1:問題文を整理する
先ほどの問題文でも、ヘンリー定数を求める条件と問題で問われている部分に分ける事ができる。
酸素は、水温20℃の水1.0Lに100kPaの圧力下で、標準状態に換算して0.031L溶解する。同じ20℃の水3.0Lに酸素は300kPaで何g溶解するか?
これを区別しておくためにも次のヘンリー表を書いておきましょう!
上の表は教えてくれた人が解いていた問題なので、下が今回の問題に関するヘンリー表です。
| 20℃/O2 | 水の体積 | 圧力 | 溶解量 |
| ヘンリー定数を求める条件 | 1.0L | 100kPa | 0.031/22.4 mol |
| 問われている部分 | 3.0L | 300kPa | nmol |
条件と問われているところが分かりやすいのはもちろんですが、ヘンリーの温度がこの表で定数として扱われているところがいいです。
ステップ2:『ヘンリーモル変換公式』からヘンリー定数を求める

ヘンリーの法則の条件文を図にすると上のようになります。ヘンリーの法則で取り出した気体は標準状態で0.031Lだとわかります。
ってことは、溶けている気体の物質量は0.031/22.4 [mol]です。
これによってヘンリーモル変換公式からヘンリー定数を求めます。
0.031/22.4=k×100k[Pa]×1.0
これを計算せずにおいておきます。
ヘンリー定数は平衡定数の一種です。てことは、
ステップ3:『ヘンリーモル変換公式』からモルを求める。

問われている部分を図に表すとこのようになります。
先ほど求めたヘンリー定数を使って「20℃、3.0×105Pa、3.0L水」に溶けている酸素の物質量(モル)を求めていきます。
nO2=$\frac{0.031}{1.0×10^5×22.4}×3.0×10^5×3.0$
です。
ステップ4:モルから求める状態量を求めていく!

さて、今回求めろと言われているのはモルではありません。「g」です。ってことは、モルを「g」に変換しなくちゃダメです。
てな訳でヘンリーの法則で求めた「モル」を「g」に変形します。酸素の分子量をかければOKです。
wO2=$\frac{0.031×3.0×3.0}{22.4}×32=0.398・・・・$≒0.40
これより0.40gです。
ちなみに、このステップ4はもはやヘンリーの法則関係ないです。例えば酸素のmolがわかったとして、体積が問われたらどうしますか?
状態方程式使うだけですよね。ヘンリーの法則がわかりませんって言う人の半分はヘンリーの法則じゃないところを質問してきます。
このステップ4はヘンリーの法則ではありません。
もし与えられている気体が混合気体だったら?
例えば、空気だったりすると、空気中のO2がどれくらいとけるか?という問題が出ればどうするか?
それは、『分圧』を求めなければなりません。
nA=kPAV水
これが公式です。
- 溶ける物質の量(nA)
- 溶ける物質の分圧(pA)
に比例するというものです。
なので、空気とかは分圧を求めなければなりません。空気などは、体積比がN2:O2=4:1です。つまりこれで分体積を表す事ができます。
分体積と分圧の相互変換する方法はこちらで公開しています!
[quads id=5]ヘンリーの法則に関する質問解答コーナー
本記事は2015年に11月19日に公開しました。もうすぐ公開して4年になります。
すると、この記事の下には大量のコメントをもらいました。(110件なう)
そこで、コメント欄の質問も見にくくなってきているのでここでまとめて行こうと思います。
圧力を求めろと言われたらどうしますか?
圧力がわからない場合どうすればいいんですか??
ーの、分圧を求めなさいのような問題があったら、ヘンリー定数っていつになっても出てきませんよね??どうすればいいですか?
分圧を求めるのに、n=kPVの公式では、Pが無いでしょ!
って言いたいんかもしれへんけど、これは記事で解説済み。¥この質問に関する答えは、別に分圧だろうと求められる。

見誤ってほしくないのは、ヘンリーの法則の目的
これは、「水に溶けている気体を取り出す」ことのみ。取り出した後はステップ4で解説しましたが
gを問われたら分子量を掛ける
体積や圧力を問われたら状態方程式に代入
めっちゃ簡単です。でもここをヘンリーの法則の問題だと思うからややこしくなるんです。
だから、ヘンリーちゃんにこれ以上求めないであげてほしい。ヘンリーは水に溶けている気体のモルがわかれば、あとは、状態方程式でP=(nRT)/Vで求められる。
なんども言いますがヘンリーの法則は水に溶けている気体の量を知るだけ。0℃で溶けてる気体があれば0℃での気体のmolしかわからない。
水温が途中で変わったらどうしますか?
水温が問題文中で変わってしまったときは、どうすればいいのですか?
そのときはヘンリー定数をとりなおせばいいのでしょうか。
とりなおすことが出来るように出題されるのでしょうか?
ヘンリーの法則は化学平衡の問題の一種です。化学平衡は「温度一定」が前提条件ですので、まず水温が変化する問題は出ないでしょう。
ヘンリー定数と言うのは、
A(気)⇄A(水)と言う可逆反応から
平衡定数をとって、
K=[A(水)]/[A(気)]から出来ています。つまり、ヘンリー定数は、
平衡定数と同様に温度によって変化します。そのときはヘンリー定数をとりなおせばいいのでしょうか。>>
ヘンリーの法則て溶質と溶媒分子の相互作用が絡んできますので、分子の大きさとかで複雑な挙動を示します。
ヘンリーの法則の温度依存性に関する問題は非常に難しくて、
量子化学計算の手法とかもまだ最適な近似が確立されてませんとりなおすことが出来るように出題されるのでしょうか?>>
おそらく出題はされないと思います。
受験生に学習してほしいのは、「温度が一定ならば」蒸気圧と溶解量の関係が記述できるということなので、大前提を覆すような問題はあまり意味ないと考えられます。
3つ目の質問
問題:酸素は0℃、100000Paで、1Lの水に49mL溶ける。0℃、500000Paで、水1Lに溶ける酸素は、0℃、500000Paで何mLか。
この問題の答えは49mLですが、ヘンリー定数を求めるやり方では49mLになりません。どうしてですか?
結果的に言うと、モルで求めようと、49mLになります。
やり方ミスってます。
随時質問回答を追加していきます。
最後に:ヘンリーの法則まとめ
- ヘンリーの法則は「押せば溶ける」というシンプルな法則
- ヘンリーの法則2つ目の定義がややこしいのは、溶ける量を体積で表しているから
- ヘンリーの法則は受験テクニック的には気体の溶けている量を知るためだけの法則
- 多くの人は気体の問題としてつまづいている
さてかなり長い記事になってしまいましたが、必要なことは全て解説できたかなと思います。世の中の解法はmolを使いませんが、この時代を生きるあなたはmolを使いましょう。
ですが、現代を生きるあなたはモルを使えばいい。そのために使う公式が『ヘンリーモル変換公式』
nA=kPAV水
これで一度ヘンリー定数を求め、求めたヘンリー定数から『モル』を求めましょう!
今日この記事を読んだあなたは、一度この記事で紹介した問題を解いてみてください。
これをする事で、あなたの力になり、試験場で使える知識になります。
[quads id=5]















圧力がわからない場合どうすればいいんですか??
ーの、分圧を求めなさい
のような問題があったら、ヘンリー定数っていつになっても出てきませんよね??どうすればいいですか?
はるかさん>>
コメントありがとうございます。
ブログ運営にいかしていきますので、
また疑問点があればコメントお願いします。
まずこの記事の問題文を見てください。
①『酸素は、水温20℃の水1.0Lに100kPaの圧力下で、標準状態に換算して0.031L溶解する。』
②『同じ20℃の水3.0Lに酸素は300kPaで何g溶解するか?』
①ヘンリー定数を求めさせる問題文
②水に溶けている気体の量を問う問題
にわかれています。
そして、「〜の分圧を求めろ」という問題文は、
②に属するので、ヘンリー定数自体は求められます。
①で求めたヘンリー定数を元に計算できます。
分圧が問われている場合、
溶けている気体のモルor質量、
または、溶けている気体を取り出したときにある圧力下での
分体積が必要になるので、
そういう問題が出る可能性は低いと思われます。
また問われてもモルが分かれば
状態方程式で変換できます。
水温が問題文中で変わってしまったときは、どうすればいいのですか?
そのときはヘンリー定数をとりなおせばいいのでしょうか。
とりなおすことが出来るように出題されるのでしょうか?
こまさんコメントありがとうございます。
水温が問題文中で変わってしまったときは、どうすればいいのですか?>>
ヘンリー定数と言うのは、
A(気)⇄A(水)と言う可逆反応から
平衡定数をとって、
K=[A(水)]/[A(気)]から出来ています。
つまり、ヘンリー定数は、
平衡定数と同様に温度によって変化します。
そのときはヘンリー定数をとりなおせばいいのでしょうか。>>
ヘンリーの法則て溶質と溶媒分子の相互作用が絡んできますので、分子の大きさとかで複雑な挙動を示します。
ヘンリーの法則の温度依存性に関する問題は非常に難しくて、
量子化学計算の手法とかもまだ最適な近似が確立されてません
とりなおすことが出来るように出題されるのでしょうか?>>
おそらく出題はされないと思います。
受験生に学習してほしいのは、
「温度が一定ならば」蒸気圧と溶解量の関係が
記述できるということなので、
大前提を覆すような問題はあまり意味ない
と考えられます。
問題:酸素は0℃、100000Paで、1Lの水に49mL溶ける。0℃、500000Paで、水1Lに溶ける酸素は、0℃、500000Paで何mLか。
この問題の答えは49mLですが、ヘンリー定数を求めるやり方では49mLになりません。どうしてですか?
この質問に関する答えは動画にしたので、
こちらの動画で確認してください。
ヘンリーは色々面倒な事が多いです。
質問者さんがおっしゃるように、
ヘンリーの法則に今回の問題を
そのままダイレクトに表す法則があります。
溶解した気体を水に解けていた気体を
みずを押していた圧力の状態で取り出すので
あればその体積は一定になる。
でも、これを考えだすと
ヘンリーの法則の超根本的な原理原則、
[A]=kPa
の『押せば溶ける』と
矛盾しているように感じて多くの受験生が
混乱しだす。
ということから、
全てモルで計算するように指導しています。
あと、モル一辺倒攻撃ができれば、
気体の溶解度の問題は、
一切頭を使わずに、ワンパターンで解けます。
ありがとうございました。今動画を見て大変良くわかりました。またよろしくお願いいたします。学校の先生よりも分かりやすかったです。すごいです。
またどんどんコメントしていってくださいね!
ヘンリーは俺もメチャクチャ混乱したので、
気持ちがよくわかったからかもです!
ヘンリー定数の普遍的な求め方を教えて下さい。「これ分のこれ」みたいな求め方はあるのでしょうか?もしくは、無いのでしょうか?教えて下さい。
na=kPaV水
なので、
k=na/PaV水
です。
水1mLに溶解する~って書いてあったらVのところに10の-3乗代入すればいいのですか?
そうです!ただ俺は1mのまま代入しますね!そしてヘンリー定数を求める時は分数のまま残しておきます。
そうするとどうせミリは消えるので10-3とか考えなくて済みます
なるほど。スッキリしました!
また質問します(・ω・)
その圧力下ときた時もn=kpvに代入すれば良いのですか?
それは問題によります。
n=kPV水のpは分圧です。
もし、問題の設定で、圧力○○と与えられていて、気体が1つしかなければ、無条件でその気体の圧力になります。
しかし、与えられた気体が、もし混合気体ならば、分圧を求めなければなりません。
セミナー例題23番
水素は0℃ 1.0×10^5Paで1Lの水に22mL溶ける
(1)0℃ 1.0×10^5Pa で1Lの水に溶ける水素はなんmolか
(2)0℃ 1.0×10^5Pa で1Lの水に溶ける水素の体積はその圧力下で何mLか
(1)はなかむら式ヘンリーで解けるんですけど(2)が解けません
お願いします
ヘンリーの法則は記事でも言っていますが、
『溶液から気体を取り出して何モルかを知るためだけの法則』
なのです。
それ以降は、ヘンリーの問題ではなく、
気体の法則の問題です。
今回は、モルが分かっているなら、
気体の状態方程式を使って
V=nRT/Pを解けば、体積が求められます。
このコメント欄にある質問に似たような質問があります。
それに動画で答えているのでそちらをご覧いただくと分かりやすいかとおもいます。
なるほどです!
ありがとうございました!
あとn=kpvにはじめに代入してkを求めるよりも 変形をして
k=n/pv=n/pv としたほうが簡単じゃないですか?
どちらでもOKです。
ありがとうございます!
とても分かりやすくて、早速使ってみようとしたところで、ちょっとした疑問が浮かんだので書かせていただきます。
n=kPV水 はヘンリーの法則から導かれたものだとは理解しましたが、V「水」となる理由が分かりません。つまり、僕は、モル濃度を「溶液」の体積あたりのモルと認識していたので、自分の中で矛盾が生じています。どう理解したらこの矛盾は解消できますか?
これはヘンリーが成り立つ条件を考えてください。
まずヘンリーは物理溶解のみ、そもそも水に溶けにくい物質です。
つまり溶ける量自体雑魚です。
さらに、気体の体積がそのまま溶液の体積にはなりません。
気体の体積は溶液の体積に比べてはるかにでかい、つまり溶解するときはもっと小さくなります。
なので溶液の体積=水の体積とみなしてオッケーなのです。
気体の体積は無視しても構わないレベルの体積でしかないのです。
質問ありがとうございます。
これも記事に加えておきます!
考えてみれば当たり前のことですよね。。。
でも改めて理解できて良かったです。回答ありがとうございます!
いえ、そういう細かいところに気付けるのはかなりセンスがいいです。
こういう説明もしていくブログにしていきます!これからもよろしくお願いします!
このブログに出会って、早速今上にあった問題を解いたのですが
解説を見ると私はヘンリー定数の時点で計算が違っていました。
n=kPVの左辺は
どうして気体の状態方程式を用いるのでしょうか。
49mL溶けるのなら
49*10^-3/22.4 molではいけないのですか。
22.4Lって101.3kpaできっちり、気体定数もちゃんと計算した時の体積であって、
今回100kPaですから厳密には標準状態ちゃいます。
さらにつぎに500kPaがでてきてそうなったら状態方程式使わざるを得ないわけですし、気体定数がでてきてとんでもない計算量になるのでやめたほうがいいです。
22.4L/molは「標準状態」と書いていない時は使わないほうがいいです。
空気の場合のn-o2の求め方教えてください
空気の場合はnO2=kPO2V水

つまり空気中の酸素の分圧を求めればできます。
なんかヘンリーに対する考え方メチャクチャ変わりました!
溶液からモルを取り出すだけ!って考えたらめっちゃ簡単に感じられました!
ありがとうございます!
そうですね!むしろ重要なのは混合気体なのです!
質問しようとしたらもう、質問コメントついていたので解決しました!
めっちゃわかりやすかったです!
結構コメントも増えて来たのでそれを見てもらうと結構解けます!
ありがとうございます!
標準状態に換算ってなんですか?
また最初の与えられる溶解度がだいたいいつも標準状態に換算して~L溶ける。とかなんですけどこれが標準状態に換算してなかったらどうなるんですか?
標準状態に換算すると22.4で割ればモルが出るよってことです。
換算してなかったら状態方程式でモルが出るよってことです。
なるほど、2個目の定義は
覚えなくて良いんですね!
molも状態方程式も知っている我々には当たり前すぎる内容だということですね
その圧力下ってそもそもどういう状況なんですか?
全圧とか分圧があってなにがなにだかよくわからなくなるんですが…
分圧ですね!
ヘンリー定数は温度が一定ならば、一定だと理解したのですが、
混合気体中の問題なんかでそれぞれの気体はそれぞれでヘンリー定数を計算しますが、ヘンリー定数というのは温度だけでなく、それぞれの気体の種類によっても変わってくるものなのでしょうか?
それはあると思います。無極性の分子でも、分枝の運動の仕方が異なったりして、様々な違いが生じると思います。
窒素は1.0×10^5Paで37°Cの血液100mLに1.40mgまで溶解する。血液の固形成分は無視できるものとし、原子量はN=14とする。
水深30mの状態から水面へ急に浮上したとき、血管内で気体となる窒素の体積は何mLか求めよ。ただし、水深30mで血液には4.0×10^5Paの圧力がかかり、空気は血液に溶けて飽和している状態である。水面では血液にかかる圧力は1.0×10^5Paである。また、血液の温度は37℃、血液の体積は4.0Lで、急浮上による変化がないものとする。
この問題の答えは1.5×10^2mL(有効数字抜きにすると154.38mL)になってたんですが、こいつをヘンリーモル変換公式で解く場合どのように解けばいいか色々試行錯誤してみたのですがわかりません。よろしければ教えてください!!
問題を解いたりはしませんがいかすみさんがどのように考えたかを言っていただければしてきはしますよ。
標準状態に換算してない?ので、PV(溶解量)/RT=kPV(水)=0.1kP
これとV(溶解量)=1.40m÷28×22.4=22.4m/20=11.2m/10=11.2×10^-4から
k=112×10^-4/RT
ゆえに水深30mで血液4.0Lに溶解しているN2の物質量は
112×10^-4/RT×4.0×10^5×4.0=112×160/RT mol
水面に出たときに血液4.0Lに溶解しているN2の物質量は
111×10^-4/RT×1.0×10^5×4.0=112×40/RT mol
よって血中から気体となって出て行くN2の質量は112×120/RT mol
PV=nRTより、V=nRT/P=112×120/1.0×10^5=0.1344 L≒1.3×10^2 mL
と考えました…
何も理解してないクソ解答だと思います。すみません。
条件文と色々ごちゃごちゃになっていると思います。
まず最初のモルはがなぜか状態方程式で求めていますが、今回gで与えられているので分子量で割れば条件式の溶解量がわかるのでヘンリー定数はすぐにわかるはずです。
今早速やってみたところk=m/10^5・2となり数値がさっぱりと合いました!!ありがとうございます。
質問ですが、モル変換公式でkを求める際の左辺の物質量は標準状態に換算したLが書いてたら22.4でわって導出、Lは書いてるけど標準状態に換算したと書いてなかったら状態方程式で導出、gや個数であれば問答無用で状態方程式とか考えず普通に分子量やアボガドロ定数でわって導出してしまえばOKですか?
そうです。ただ、この文章からは、ヘンリーのときは特別な事をしていると言う雰囲気が感じられますが、別にただモルを求めているだけです。
間違っていないけど考えのずれを感じます。
こちらをお読みください。
理論化学計算で意識する2つのこと
昔の僕が意味わからん質問してしまってすみません。本当、どんな問題も結局はモル利用・モル比ですね。現在なかむらさんのブログ見ながらセミナーがつがつやってます。化学は計算問題がクソ意味不明で苦痛でしかなかったんですが、今は発展問題もサクサク解けてたのしいです。本当にありがとうございます!!
おお!良いですね!その調子で頑張ってください!
[A(水)]=nA/V水=kPA の式がよくわかりません。どういう意味なんでしょうか?
[A(水)]はモル濃度です。水に溶ける濃度は、kPaです。kは比例定数です。なのでPaというモル濃度に比例します。
基本的な質問に丁寧な対応ありがとうございました。
もう1つなんですが、混合気体の問題を解いているのですが、このような問題の考え方はどうしたらよいのでしょうか。ヘンリー表の書き方もイマイチです。
窒素は40℃、1.0×10^5Paにおいて水1.0Lに5.5×10^-5mol溶ける。40℃で1.0×10^5Paの空気が水に接している時、10Lの水に溶解している窒素の質量は何gか。ただし、空気は窒素と酸素が体積比4:1の混合物である。
まず分圧に比例するので分圧を求めることから始めましょう。
ヘンリーの法則の圧力は、分圧です。
返信ありがとうございます。
体積比から窒素の分圧が8.0×10^4Paと出せました。
それでヘンリー表の条件の部分は体積1.0L、圧力8.0×10^4Pa、溶解量5.5×10^-4molで、問われてる部分は10L、8.0×10^4Pa、n molでいいんでしょうか??
答えが合わなくて悩んでいます。
いや、条件式は窒素だけの話ですので、1.0×105Paです。条件式では空気とは書かれていません。
そして求めるときは空気なので窒素の分圧を求めなければならないのです。
こんにちは
質問です。
200mlの炭酸飲料を0℃、100KPaの二酸化炭素で開栓すると、二酸化炭素が86ml出てきた。開栓前の炭酸飲料の二酸化炭素の圧力を求めよ。 ただし、0℃、100KPaで水1mLに二酸化炭素は1.72mLとけるものとする。
これが問題集の解法ではわかるのですが、なかむら公式だとわかりません。質問欄もみたのですがダメでした。
お願いします。
動画 ヘンリー法則に期待するな! をみたらわかりました。
自分は式を立てる順番と代入の仕方が間違っていました。
そうなんですね!良かったです!
質問させていただきます。
CO2 の純水に対する溶解度
(標準状態に換算した値)
10°C 1.2L
10°C 1.0×10 5乗Pa において
フタが付いた容器に純水1Lを入れた。
この容器にCO2を6.4L入れた。
しばらく放置するとフタが下がり
平衡状態に達した。
このとき CO2の体積は 5.2Lになった。
この後 10°Cに保ったまま圧力を
2.0×10 5乗 Pa にして放置すると
CO2の体積が X Lになった。
10°C 2.0×10 5乗 Pa のとき
CO2の体積は 1.24L というところまでは分かりましたが、
解説では この後
10°C 1.0×10 5乗 Pa に換算して
最終的には
(6.4-2.48)×1/2 ≒ 2.0L (答)
となっています。
何故 1.0×10 5乗に換算するのか
よく分かりません。
もし先生流の別の解法があれば
教えていただきたいです。
解法というより、
その問題が何を問われているかによりますよね。
その問題が、1.0×105Paのときのの事を聞かれているとしたら、
換算する必要は在ります。
このコメントに書かれている内容だけでは、なぜ、1.0×105Paに換算するのかはわかりません。
問題文は上記の内容しか
書いていないんです…汗
1番冒頭に 『1.0×10 5乗Paにおいて』と書いてあるから でしょうか?
あと何故最後 1/2にしているのかが
わかりません
ごめんなさい、それならちょっとわからないです。
それは1.0×105Paに換算したからです。
なかむらさんの解き方を見て思ったのですが、
標準状態に換算すると、
溶解する気体の物質量=(体積は何倍に増えたか)×(圧力は元の何倍になったか)×(最初の物質量)
と、捉えていいですか?
分かりにくくて申し訳ないです。
いいけど、この記事の主旨には合わないです。
それでバッチリ理解できるならいいんじゃないですか。
ただ、理論化学ってmolに換算して計算するものなので、わかりやすいのでこれにしています。
ご自由に
ヘンリーの公式をmolで解釈し、またヘンリーの条件を表をかいて書き込むだけでこんなに簡単にもとまるなんて本気で感動しました。これまでは重問の解説を読んだりヘンリーがわからなくて学校の先生に質問したりしたのですが、なんか計算が面倒だなぁと完全に納得できてませんでした。本当にありがとうございます!他の分野のところも学ばさせていただきます!
ありがとうございます!
これからもお願いします!
水xmlに溶ける気体の体積が、標準状態に換算されてない場合は、どうすれば良いのでしょうか?
状態方程式で求めてみてください!
なかむらさんが説明の時に挙げてた例題で100kPaを公式のpのところにそのまま代入していらっしゃったんですが100000pに直して計算しなくていいんでしょうか?そもそもヘンリーの法則のpの部分の単位はkPaということでしょうか?
直さなくてもいいです。両辺kPa使えば約分されるからです。
ヘンリーの法則の質問の動画で
左辺のモルを気体の状態方程式で表すときに気体定数を使ってましたが、与えられてないときでも8.3×10^3使ってよいのでしょうか?
消えるな〜と思っていたので使いました。Rと置いておけば良いと思います。
質問とかじゃないんですが、あまりにも分かりやすくて興奮してます。笑
今まではこうヘンリーの法則だけ教えられて、
結局受験でどう使うん!?って思ってたんですけど、これみて色々納得しました。
ありがとうございます!助かりました!
ありがとうございます!励みになります!
コメント失礼します。
このような複雑な問題はこの公式を使えば楽だとわかったのですが、
単純な問題は公式を当てはめたほうがいいですか?(分圧が一定など〕
コメント失礼します。
質問3の問題にて、最初の段階でnを求める際にPV=nRTのVに「49ml」と代入していましたが、単位は[L]だから「49/1000L」ではないのですか?
初歩的な質問ですがよろしくお願いします。
mLであえて計算しています。49/1000は計算がしにくいです。補助単位の部分を御覧ください
回答ありがとうございます。
mLで計算をしたら答えが合わなかったため上記の質問をしましたが、計算ミスをしていました。
大変失礼しました。
補助単位とても参考になりました、すごく便利です!
はじめまして。混合気体の溶解について質問させて頂きます。
溶解度が酸素:0℃→4.9×10^-2、20℃→3.1×10^-2
窒素:0℃→2.3×10^-2、20℃→1.5×10^-2
溶解度はその気体が1.01×10^5Paで接している水の1mlに対して溶解する気体の体積を、標準状態での値(ml)に換算して示している。
20℃で1.01×10^5Paの空気中に水1Lを置き、気体が飽和するまで溶解させた。この温度において水に溶解している酸素に対する水に溶解している窒素の物質量の比は、空気中における酸素に対する窒素の物質量の比の何倍か求めよ。ただし、空気中における酸素に対する窒素の物質量の比は4(酸素:窒素=1:4)であるものとする。
という問題でなかむら先生のヘンリーモル変換公式とヘンリー表を使って解きたいのですが、1Lやら1mLやらでよく分からなくなりました。この問題のヘンリー表の書き方とヘンリーモル変換公式の当てはめ方を教えて頂けますか?長々とすみません。よろしくお願いします!
p.s.
「ヘンリーの法則に分圧が絡む問題」の動画を拝見してヘンリー表を
20℃ O2条件:水→1.0×10^-3L、圧力→1.01×10^5×4/5Pa、溶解量→3.1×10^-2×10^-3/22.4mol、問:水→1L、圧力→1.01×10^5×4/5Pa、溶解量→xmolとおく
20℃ N2条件:水→1.0×10^-3L、圧力→1.01×10^5×1/5Pa、溶解量→1.5×10^-2×10^-3/22.4mol、問:水→1L、圧力→1.01×10^5×1/5Pa、溶解量→ymolとおく
と考えてみたのですが…。どこが間違っているかご指摘お願いします!
溶解する気体の、分圧下での体積を求める問題でつまずきました。
なかむらさんが回答された上の質問では、PV=nRTのうち、nだけが不明で、PV/RT=kPaV水 の方程式でkを求めていましたよね。
しかし、私がといた問題では、nはわかっていて、かつ、PV=nRTのPがわかっていないので、k=PaV水n でkを求めました。
そうすると、そのあとの分圧下での体積を求める段階で、kの式の中にRTが含まれていないためにうまく消えませんでした。頑張って計算すると近い数字にはなるのですが…。うまく消える他の方法がありますか?
k=PaV水n この時点で間違えています。
すみません、k=n/PaV水 でした。打ち間違いました。k=n/PaV水だったので、もう一度質問に回答していただけますか?
モルを求めてから状態方程式で圧力に直せばいいです。
なので公式は常にモルを求めるために使ってください。
今までなんとなくしか理解できてなかった部分がちゃんと理解できてすっきりしました!!
条件に当たる部分と問題で問われている部分とをしっかり区別して解けるのでわかりやすかったです
ありがとうございます
20℃、1.0×10^5Paで水1mlに二酸化炭素は0.87ml溶ける。今、体積比で2:3の二酸化炭素と酸素の混合気体が、20℃、5.0×10^5Paで水に接している。この水10mlに溶けている二酸化炭素は何gか。ただし気体定数は8.3×10^3Pa·L/mol·K、原子量C=12,O=16とする。
この問題で自分はヘンリー定数を出すためにk=0.87/(1.0×10^5×水1ml×22.4)を求め、Wco2=44×k×5.0×1.0×10^5×2/5×10×10^-3というように答えを出したのですが、間違っていました。
気体定数が与えられていてダミーかなと思ったのですが、解答ではちゃんと気体定数も温度も使っていて状態方程式を利用していました。今回のように22.4L/molが消えそうにない場合は状態方程式を使わないといけないのでしょうか?
そもそも標準状態じゃないから22.4L/molは使えません。
あ、この記事に載っている問題はよく見たら20℃のものでも「標準状態に換算して」と書いてあるのを見落としてしまっていました…
返信いただきありがとうございました。
ヘンリーの法則って大っ嫌いで何に言ってるかわからなかったのに、スッキリとわかりました!!ありがとうございました!!
質問なのですが、
ヘンリーの法則のところの問題で(1) でmol (2)でその分圧下で何mlか求めよと出てきたのですが どのように求めれば良いのでしょうか、気体の状態方程式使うのですか?
そうです!
窒素N2は、温度0℃、圧力1.013×10^5Paにおいて液体の水1Lに1.0×10^−3mol溶ける。はじめ、液体の水10Lの入ったピストン付きの容器に0℃、1.013×10^5Paの窒素N2 11.2Lが接し、溶解平衡に達していた。ピストンを押し込み、温度0℃のままで窒素N2の圧力をはじめの圧力の6倍にすると、気体部分の体積は何Lになるか。ただし、水の蒸気圧と体積変化は考えなくてよいものとする。
答 1.7L
という問題があるのですが解説のように解こうと思ってもやり方がわからなくなってしまいました。
教えて欲しいです。
ヘンリー表で条件の溶解量が0.031/22.4molとなっていますが、20℃(標準状態でない)なのに22.4Lで割ってしまうのはなぜですか?
標準状態に換算して0.031Lと書いてありますよ。
標準状態の時はmolを22.4L/molが使えてLに換算できるのは分かるのですが、標準状態ではない時にはどうすればLに換算できるのでしょうか?
PV=nRTに、代入で出ると思います
記述式だった場合この解き方で書いて構わないのでしょうか?
構わないです。
ヘンリーの法則の問題で、「気体Aが○mol封入してある体積V(L)の容器に水x(ml)を入れました。」という内容で水の蒸気圧も考慮するバージョンの問題についてです。疑問に思ったのが、気体となってる水を無視しないのなら、「水x(mL)」という表現はある意味「水(気)(mL)+水(液)(mL)」ということでしょうか?そもそも同じmolにおいて、気体と液体では体積はまったく異なると思うのですが…。仮にそうだとすると、気体Aは水(液)に溶けるわけですから、気体Aがx(mL)の水(液)に溶けている、という表現は少し違うような気がするのですが、解答はこのようになっていました。一部は水(気)になってるので、気体Aが溶けている水(液)の体積はx(mL)よりも小さい、と考えてしまうのですが…。
水の蒸気圧を無視できる問題ではこのようなことは考えないのですが、考慮する場合だと混乱してしまいます。とんちんかんな質問だとは思いますが回答宜しくお願い致します。
あの、条件と、問題見極めのやつで、mol(条件)のやつに、水の体積から×3、圧力に比例するから300/100で、×3すればヘンリー定数求めなくてもmolは、出ますよね?ヘンリー定数が、必要不可欠な問題ってどういう問題ですか?
別のコメントで回答済み。
この解法を知ってから、解ける自信がつきました。
ほとんど頭を使わずに解けるなんて、、!
本当に助かりました。
窒素と酸素の体積比が4:1である混合気体が25度101300Paのもとで水1ℓに十分な時間接触してるとき、水に溶けている窒素と酸素の質量の比を求めよ。ただし溶解度は1ℓで窒素0.014ℓ、酸素0.028ℓである。
これってヘンリーですか?
水と接触とか、いまいち状況がつかめません。
すいません、ちょっと分からないことがあります。
n=kPVで水に溶けている気体の物質量を求める時に、
Pに当てはめるのは
「封入した時の気体の圧力」か「溶解平衡に達した後の気体の圧力」のどちらでしょうか?
理由も教えて頂けると嬉しいです。
とてもわかりやすくて感動しましたが実際にこれを記述式のテスト(大学入試)などでは
使っていいのですか?
また、使う際はどうやって記述するんですか?
質問です
酸素は1.0×10⁵のとき、0℃の水に49ml溶ける。
2.0×10⁵Paの酸素が水10Lに溶ける体積は、
0℃、2.0×10Paのもとでは何mlか。
という問題の答えが回答と合いません。
どのように解いたらよいでしょうか。
例題のことについて質問なのですが、
標準状態と記載されていて22.4L/molを使うことはわかり計算も合いました。
ただ解説の中で、300kPaのkは相殺されるとおっしゃっていたのですが、なぜそうなるのかがわかりません。
0.031Lを31mlとおいてmとkが消し合うのならわかるのですが、なぜ相殺されるのですか?
問題:酸素は0℃、100000Paで、1Lの水に49mL溶ける。0℃、500000Paで、水1Lに溶ける酸素は、0℃、500000Paで何mLか。
この問題の答えは49mLですが、ヘンリー定数を求めるやり方では49mLになりません。どうしてですか?
これは上の方に載っていた”あつこ”さんからの質問です。
この質問に対しての解説動画では、ヘンリーの式の、左辺のnを、気体の状態方程式を使って求めています。
なぜ、左辺のnについて、
モル利用(49/22.4)を使えないのですか?
左辺のnの求め方について、使い分けがあるんですか?
別コメントで回答済みです
見てきました。
納得できました。
有難うございます。
質問したいことがあるのですが、ヘンリーのmol公式は計算過程を記述しなければいけない問題の場合、採点者側が知ってて当たり前のものとして扱っていいのですか?それとも、ヘンリーの法則よりn(A)=[A]pAが成り立つことをちゃんと記述しなければいけないのですか?
質問したいことがあるのですが、
ヘンリーのmol公式って計算過程を記述する問題のときは当然のものとして扱ってよいのですか?
それとも、ヘンリーの法則より、n(A)=[A]paが成り立つことを言わないければいけないですか?
気体Aの水への溶解にはヘンリーの法則が成り立ち、温度32℃、圧力1.0×10∧5Paのとき、水1Lに0.050L溶ける。内容積の調節可能な容器に1.0molのAと10Lの水を入れた。32℃
、1.0×10∧5PaのA1molの体積は25Lとして次の問いに答えてください。
(1)容器内の圧力が1.0×10∧6Paのとき、Aの溶解後の気体部分の体積は何Lですか?
(2)Aの溶解後の気体部分の体積が4.5Lのとき、容器内の圧力は何Paですか?
(3)0.4molのAが水に溶けたとき、容器内の圧力は何Paですか?また、Aの溶解後の気体部分の体積は何Lですか?
ヘンリーの法則でよくわかりませんでした。解説お願いします。
どこに質問すればいいか分からないのでこのページで質問させていただきます。
立方体のプールの底面から空気を送り込んで溶解平衡が成立した時、プール内の水に溶けているo2の量を求めるという課題があるのですが、どのように解けばいいでしょうか?
よろしければご教示ください
なかむらさん、この質問は授業で解説されたので解決致しました。折角返信頂いたのに申し訳ありません。
私は返信していないので大丈夫ですよ。
返信ありがとうございます。
すみません、空気送出口は立方体の真ん中にありました。水は循環するという条件と、気温、気圧、その時の溶解度が与えられており、私は体積×溶解度でやったのですが間違いだそうです。空気送出口の上下で計算方法を変える必要があるようなのですが、よくわかりません。空気を送り込む圧力も考慮する必要があるのでしょうか。
条件文により求めたヘンリー定数が変わらず問題文の方でも使える理由が視覚的によくわからないのですが何故なんでしょうか?
温度一定だから。
ヘンリー定数が「平衡定数の一種」と書いてあるでしょ?