こんにちは。
溶液が苦手な人は多いですが、
おそらく問題に出て来てなくて、
あまり得意ではないというのが、
実態だと思います。
また、浸透圧が何なのか?
ぼんやり覚えているのです。
ここではっきり言いたい!
3つの定義覚えろ!
と!
これをちゃんとやれば、
そんなに大した事無いよ!
ってことをわかってもらおうと
思います。
でも、浸透圧のまえに
色々知っておかんとあかんモノが
色々あるので、
それをまず知って行きましょう!
目次
半透膜と全透膜とは?
半透膜というのは、
お前は通っていいけど、
お前はダメだ!って言います。

溶液中の特定の粒子だけを
透過させます。
例えば、セロハン膜で
水とデンプン水溶液をわけたとします。

こういう、水は簡単に
行き来でいますが、
デンプンは通れません。
このように、粒子の大きさで
通れる奴と通れない奴を
区別されます!
浸透とは?

浸透とは、格差是正のために、
貧乏人が移動する事です。
溶液の濃度が大きい方に、
溶液の濃度が小さい方が
移動します。
そして、なんとか、
全員同じくらいの所得にしましょうね!
って言う技です。

このように、
いっぱい粒子を持っている人を
薄めて、みんな同じくらいにしよう
というのが浸透です。
税金みたいなモノです!
日本の税収入はこちら、

高所得者からは、
45%も奪って、
メチャクチャ薄めて、
なんとか平等にしよう!
というのが所得税です。
話がそれたか、、、
ぼんやり覚えるからあかんねん!浸透圧の定義3つ覚えろ!
浸透圧って、結構ぼんやり、
わかっているんです。
ですが、ここでは3つの定義を
明確に覚えてもらいます。
「なるほど、
この3つ全部同じって事なんやな!」
と言う風にきっちり理解する事が
非常に重要です!
なので、
3つとも覚えましょう!笑
浸透圧の定義①おい、入ってくんなや!帰れ!力
浸透圧の1つ目の定義は、
こちらです。

このように、溶液と
純粋な溶媒を半透膜で
区切ると、
どんどん浸透してきますよね!
これを元の高さまで戻そう!
逆側の溶液を押します。
そして、同じ高さになるまで押さえつけるのに
必要な力。これが、
『浸透圧』なんです。
これが1つ目の定義です。
浸透圧の定義②貧乏人の金持ちを引きひきずりおろしてやるという意思力
次は、貧乏人がなんとしても、
金持ちとの格差を埋めてやろう!
という気持ちで、金持ちのエリアに
侵入して行く時の力です。

なんとか、金持ちの金を
少しでも貰いたい!
と思って、濃度が大きい方へ、
濃度が小さい方から移動しています。
浸透圧の定義③審判が測定した記録!
浸透圧の定義③は、
主役が変わります。
今回の主役は、
『半透膜』です。
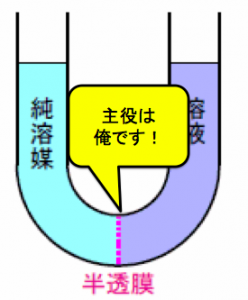
この半透膜が審判として判定するわけです。
ここで重要な考え方として、
溶液側から溶媒側へも、
すこしは、浸透している!
と言う事です。
これは、平衡の考え方と
似ています。
平衡状態と言うのは、
反応が止まっているわけではなく、
正反応と逆反応が起っているけど、
同じ分起っているから止まってるように見える
のでした。
結構これに近いです。
この浸透という現象も、
純溶媒→溶液の流れが
大きすぎるから、
溶液→純溶媒の流れが
見えなくなっているだけ
なのです。
つまり、
両方向起っているけど、
片方が大きいからもう片方が見えない
だけなのです。
というわけで、

このような画像になります。
で、この2つの和をとると、
半透膜的には、実質、
この力を受けているのに
代わりがありません。

この実質的に押す力を
『浸透圧』と言います。
浸透圧が何か良くわかる実例
浸透圧って実際、
こういうU字管の実験とか見るより、
実際の現象を見た方が、
わかりやすい!
キュウリの漬け物
なかむらは非常に
キュウリが嫌いなので、
この神聖なるこのサイトを
キュウリで汚すのは非常に
心苦しいが、

このようにキュウリを
塩水とかに付ける事にします。
キュウリのなかには、
水があります。
そしえ、キュウリの細胞膜は、
『半透膜』です。
なので、
半透膜からはガンガン水が
抜けていきます。
だから、キュウリの漬けもんって
なんか縮んでますよね。

あ〜画像見ただけで匂ってきた、、、
と言うわけで、
キュウリの塩漬けも
浸透圧が絡んでいる現象でした。
ナメクジ
ナメクジを使ってこういう感じです。

まあナメクジも全然好きじゃ
ないので、
あまり見たくもないですが、
ナメクジに塩をかける実験を
した事がある人は沢山
居ると思います。
このナメクジに塩をかけると、
しぼんでいくこの現象、
これこそ浸透圧なんです。
この動画のように、
塩をかけると、
ナメクジの細胞から、
水がどんどん抜けて行きます。
浸透圧の計算方法
さあそれでは、ようやく浸透圧の
計算に入って行きます。
浸透圧の計算はまず、
ある公式をおぼえるところから
入ります。
初めて習う人でも、
「あ、見た事ある!」
ってなります!
ファントホッフの法則
溶液の浸透圧をπ[Pa]として、
この浸透圧は、溶媒や
溶質の種類に関係なく、
モル濃度C、絶対温度T(K)に比例する!
そして、
πは、希薄溶液(濃度が十分に薄い溶液)では、
CとTに比例します。
その公式が、
π=CRT
となります。
で、今まで溶液の分野で
凝固点降下、沸点上昇
などでは、
濃度を質量モル濃度を使って
いましたが、
今回は、『モル濃度』です。
ってことはやで!
C=n/Vってことも出来るんちゃう?
n(溶質のモル)
V(溶液の体積)
これをファントホッフの式に代入すると、
πV=nRT
という式になります!!
めっちゃ状態方程式見たい!!!
すごい!!!!
不思議!!!!
(ちなみに、気体の状態方程式と
同じような形になるのは、
同じ近似を使っているので必然です)
(でも受験生にわかるようなことでは
ないので、
「え〜すご〜い気体の方程式とおんなじ〜!!
化学って不思議〜!」と思ってて下さい!)
気体ちゃうのにR気体定数を
使うんです!
不思議ですね〜〜笑
ちなみに、
凝固点降下&沸点上昇では、
電離や会合を考えました。

浸透圧も同じように
電離も会合も考えます。
浸透圧から分子量測定も可能
浸透圧から分子量を
求める方法も実際に
構造決定の最初に出題される
事もあります。
πV=nRTの式を見ると、
n=w/Mですよね。
w(溶質の質量)
M(溶質の分子量)
これをファントホッフの式に代入すると、
πV=(w/M)RT
となります。
これから、
M=(wRT)/πV
という式が導かれます!
これより、浸透圧がわかれば、
分子量を求められるので、
構造決定の最初の方に、
出てくる事もあります!
浸透圧の測定
浸透圧の測定には、
2パターンの装置を
使います。
ですが、2パターンあるものの、
結局測定している物は、
同じです。
まずは装置の2パターンをご紹介します。
用いる装置①U字管
先ほどから何度も出てくる、
あのU字管です。

このU字管の真ん中を半透膜で
区切ります。
そしてその両側に、
溶媒と溶液を入れます。
わかりにくければ、
溶媒=水
溶液=食塩水
をイメージしてください。
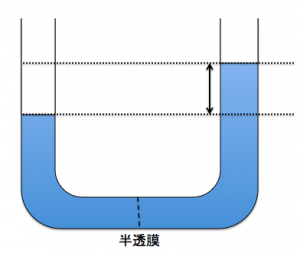
半透膜の両側を同じ高さに合わせます。

そして、これをしばらく置いておくと、
溶媒から溶液の方へ浸透し
次の図のようになります。

つりあったときに
溶液の濃度を薄めようと、
図のように液面の差が
できます。
そして、あとから取り扱う、
液面の高さから浸透圧を
求める方法をお教えします。
用いる装置②なんかこんな感じの装置
このような器具を使います。
これも半透膜を通って、
侵入していきます。
溶媒から溶液の方向へ、
どんどん侵入して行くと、
その浸透圧の分だけ、
溶媒面(水面)から持ち上がります。
この高さを測定するのです。
液面差からどのように圧力を求めるのか?
この計算テクニックは是非覚えて
置いてほしいです。
初見では、
「え、なんで水銀柱の情報が与えられてるの?」
と混乱してしまいます。
今日はそれを説明していくので、
覚えておいてほしいです。
液面の差をh[cm]とします。
hcmの溶液中が示す圧力が、
浸透圧に一致します。
このhcmの溶液中が示す圧力は、
溶液中の高さh[cm]と
溶液の密度d[g/cm3]に比例します。
よって1.013×105Paを示す
水銀柱の高さが76.0cmで、
水銀の密度が
13.6g/cm3
よって、浸透圧は、
次の計算で求める事が出来る。

よく詰まるのが、
水銀柱の高さに換算するところ
です。
というか、
換算と言うものがわかりにくい、
なので、具体例を出して
イメージを掴んでほしいです。
例えば、メートルをキロメートルに
換算すると、
つまり、ある長さxメートルと言う
長さがあれば、
キロメートルにするときは、
x/1000キロメートルとなりますよね。
式で表すと何をしているかというと、
こういう事をしています。
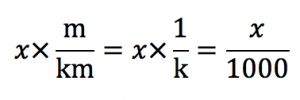
というわけで、
メートルをキロメートルに換算する
には、
メートルをキロメートルで割った物を
掛けているのです。
てことは、
溶液の高さを水銀柱の高さ
にするには、何かしら

をかけなければなりません。
で、今回密度を掛けます。
すると水銀の高さに換算する事が出来ます。
すると水銀に換算した高さがでるので、
これを高さから、
圧力に換算します。
そのために、
高さ→圧力に換算したいので、
×圧力/高さと計算しました。
すると、圧力から高さを
求める事が出来ます。
つまり、浸透圧の実験の問題では、
『液面差の長さ』と『溶液の密度』などの
情報があれば、
液面差を圧力に換算する事が出来る!
と言う事がわかります。
いかがでしたか?
浸透圧のことを全てマスターできる用に
記事を作って参りました。
なので、次は、浸透圧を
マスターするために、
浸透圧に関する過去問で
練習して行きましょう!















高さ→圧力に換算するのに
×高さ/圧力 ではないのですか?
なるほど、
高さ×高さ/圧力=(高さ)2/圧力
になります。
ごめんなさい。返信された内容と、
h×d/13.6×1.013×〜の式をつなげることができないです
その質問ですね。
それに関しては全く次元の違う話です。
水銀の高さの圧力の単位でもあるのです。
そして水の高さを水銀の高さに変えてそれをPaに変えているのです。
わかりにくかったですか?
わかりました!
溶液の高さ→水銀の高さ に換算する時は、溶液と水銀は別物だから
h×溶液(密度)/水銀(密度)をして
水銀の高さ→水銀の圧力への換算は
同じ水銀同士だから
水銀の高さ×{圧力/高さ}を計算する。
という解釈でいいですか?
そういうことです!
スッキリしました!
ありがとうございます
A側にはNaCl0.2mol/Lとタンパク質1gB側には蒸留水100mLの浸透圧で 27℃ 10㎝の水柱に相当する圧力がありA側のタンパク質の分子量はおおよそいくらか?(1×10⁵Pa=1034cm水柱、気体定数=8.3×10³Pa・L/(K・mol)) という問題でNaClのことは触れずにタンパク質の質量とその時の圧力、温度でファントホッフの式に代入しているのはどうしてですか?NaClはなぜA側にいれたのでしょうか? また、別の問いにNaClはイオンなのでセロハン膜を通るとあるのですが、、、半透膜でなくセロハン膜であるからですか?長文失礼しました!
そうですね、セロハン膜だからです。
セロハン膜は、Na+やCl–を透過させてしまいます。
浸透圧の例としてナメ○ジを出すのはわかりますが、生物の中で最も嫌いなものなので消して欲しいです。自分勝手ですみませんが、よろしくお願いします。
知らんがな。
失礼します。
U字管の装置について、左右の液面の高さの差がhになったとき、高さhの液柱に働く重力の大きさと純溶媒が溶液に浸透しようとする際の力の大きさが等しくなっていると考えたのですが、このとき左右の液面にかかる大気圧は等しいとみなしています。この認識は正しいのでしょうか?
正しいです。液面差hの液柱の水圧と浸透圧が等しくなります。
セロハンが通すものと通さないものの違いって何ですか
大きさです。
単位を見てて思ったんですが、もしかして密度って加速度をかけてやれば圧力になるってことですか?この問題だと、分母分子両方に重力加速度がかかるので、約分されてると見てもいいのでしょうか?
そうなら、密度×高さの比=圧力の比として納得できる気がします!
距離を表すものが違うのでそれは無理だと思います。
返信ありがとうございます!
cmとmとで違うということですよね?それこそ換算してやれば、うまくいきませんか?もしかして、同じ単位で異なる概念の量を表すこともあるんですか?
それとも、
(左辺)=(水銀柱の密度×高さ×g)/(溶液の密度×高さ×g)
=(水銀柱の密度×高さ)/(溶液の密度×高さ)
(右辺)=(水銀柱の圧力)/(溶液の浸透圧)
これなら左辺右辺それぞれに関して単位はなくなります。うまくいきそうな気もしますが…
cmとmが違うという話ではありません。
加速度のmは物体が進んだ距離ということなので、
この話とは全く異なります。
正しくは密度×高さ×加速度が圧力と同じになるのか、ということです
(注)定数倍のものを、「反映している」と表現してます&曲解多いのでうのみにしないでね
浸透圧で高さを考えるときは問題文とかにU字管の断面積が一定とかいう前提が書いてあるのでは?
だから液面差が(断面積×高さ)である体積の差をダイレクトに反映していて、そうなると(密度×高さ)が(密度×体積=質量)を反映してることになる。質量は動きにくさだから、ある高さの液面差を作るとき、どれだけ動かしにくいのかというのを数値化したのがU字管の浸透圧を考えるうえでの密度になると思います(たぶん)
ここでの浸透圧の定義①でいえば(純溶媒が追い払った高さ)が(半透膜の向こう側に追い返された人数)を反映し、密度が(一人当たりのてこずらせよう=質量)を表しているとも受け取れる(かも?)
重力加速度は単位として(N/kg)でもあり(単位質量当たりにかかる力)を表しているから、(密度×高さ×重力加速度)が、断面積が一定である状態での(追い返し力=浸透力)みたいなのを表し、それは単位面積当たりの力=浸透圧ってことだと思います。
あと、思い付きですが密度は単位体積当たりの質量、つまり同じ大きさで比べた時の動かしにくさの尺度を表しています。強引かもだけど浸透圧の定義③でいえば溶液が純溶媒に比べて十分に密度が高いなら溶液からのそのそ半透膜をこえて純溶媒にいこうとする人は純溶媒から溶液にいくより少ないだろうし、これは最後に出てきた式で浸透圧と溶液の密度が比例してる理由になると思いました。
釣り合った時に
溶液側に少量の溶質を加えるとhが大きくなり、
純溶媒側に少量の溶媒を加えるとhが小さくなる、
という問題を解いたのですが、後者を間違えてしまいました。
両方とも大きくなると答えてしまいました。
濃度の差が両方とも広がると考えたのでそう答えたのですが…
ちなみにその解説にはどちら側に少量の溶媒を加えてもhは小さくなる、と書いてありました。よくわかりません。
(注)結局自分も混乱しているので質問も兼ねてます笑
純溶媒中の溶質の濃度は0%、溶質を加えれば濃度差が縮まり溶媒を追加すれば単純に純溶媒側の水面が上がって液面差が縮まるからどっちにしろ純溶媒には溶質を加えようと溶媒を加えようと一緒、結局溶液側のcが変わらないからΠ変わんないみたいですね。純溶媒側の浸透圧はΠ=0×RT=0で溶媒を追加しても濃度が一定であることが感覚と反してるように思う原因なんでしょうね、とおもったけど定義①でいくと純溶媒のかさが増えた分だけ重くなるような気が…
>渡辺先生、純溶媒に溶媒を追加しても純溶媒側の水圧が上がって浸透圧は大きくなりそうですがどうなんでしょうか。それとも「少量の溶媒を加える」だから無視できる的な感じですか?
あとこれとは別に、純溶媒ではなく濃度差のある同じ溶質の水溶液であれば単純に同じ濃度になるまでどちらかに溶媒が移るから、単純に液面差がある同じ濃度の水溶液ができますよね?この場合、液面低い方(分量少ないだけで濃度は一緒)に水入れると濃度差で液面差は広がると思うのですが、これも水圧とかを考えたら自信なくなってきました。
わかりやすかったです。
ありがとうございましたm(__)m